大家好呀,上期介绍了什么是数字签名和ECDSA,本期带大家了解一下ECDSA的原理。(友情提醒:请备好晕车药和垃圾桶)
基础数学与二进制
ECDSA只使用整数,没有浮点数(这意味着可能的数值是1,2,3……,但不可能是1.5,2.5……),而且整数的范围受到签名中所使用的比特位数的限制,使用更多的比特意味着更大的数字范围,也拥有更高的安全性能,因为这使得“猜”到方程当中所采用的具体数字变得更难。
众所周知,计算机采用比特来表示数据,一个比特是二进制的“数字”(0和1),八个比特表示一个字节。
每次你增加一个比特,可表示的最大整数就可以翻一倍:
使用4个比特,你可以表示0~15,一共16个数字,
使用5个比特,你可以表示0~31,一共32个数字,
使用6个比特,你可以表示0~63,一共64个数字……
因此,8个比特,即1字节,可以表示256个数字,32字节,则可以表示4294967296个数字……通常ECDSA会总共使用160比特,它可以表示相当大的数,可以有49位数字在里面。
另一个你需要知道的知识点是数学里的模运算,简单的说,它是整数求除之后的余数。
举个例子,x mod 10意味着x除以10的其余部分,它将始终是0和9之间的数字,所以142 mod 10的结果是2;另一个例子是x mod 2,如果x是偶数则结果为0,如果x是奇数则结果为1。
ECDSA方程
现在言归正传,ECDSA是如何工作的呢?首先,椭圆曲线密码学是基于下面的一个方程式: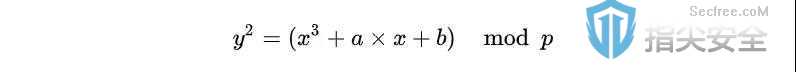
你需要注意的是,有一个模运算(mod),并且 y 是平方的(不要忘记这是图上曲线的方程),这意味着对于任何x坐标(不要忘记,我们只使用整数),将会有两个y值,并且曲线在X轴上是对称的。方程中模的底数p是一个素数,并确保所有的值在160位的范围内,它允许使用模平方根和模的乘法逆元来简化运算。
由于我们有一个模(p),这意味着 y ^ 2 的可能值在 0 和 p-1 之间,这之间便是所有可能的值。因为ECDSA规定只能是整数,只有那些值较小的子集才能构成一个“完美平方”(两个整数的平方值),这给了 N 个可能的点,其中 N






